You can't spell VEGAS POKER without E-V and R-A-K-E
Public poker tournaments aren't necessarily tougher than basement home game ones, but they're definitely harder to beat
I’m headed to the World Series of Poker tomorrow morning! Will be there for about a week, with no set plans except to play WSOP Event #75, the $1K Tag Team with my friend Danny next Monday, and to play Coach’s $8-$16 17-game mix at Resorts World on Saturday. I’m likely to fire a few bullet in WSOP Event #70 ($400 Colossus) over the weekend, but otherwise I’ll be looking around for interesting tournaments, games, and/or adventures. If you’re gonna be in Vegas and want to meet up, let me know.
A buddy of mine who’s a casual poker player asked me an earnest question last week: how tough is the competition at the World Series of Poker?
It’s a good question. Some of the tournaments—like Event #55, the Super High-Roller that costs $250,000 to enter (yes, $250k!)—are filled almost exclusively with the very best professional players in the world. Other tournaments—like the $400 Colossus or the various low-buy-in Daily Deep Stacks—more closely resemble the skill of a serious-ish neighborhood basement game, with some not particularly good amateurs and other pretty decent (for amateurs) amateurs.
Many of the tournaments—especially the ones with $1,000 or $1500 buy-ins—fall in the middle, with lots of pretty weak players but also lots of serious professionals and high-level amateurs. And the $10,000 WSOP Main Event is famously full of amateurs who don’t really belong in tournament that expensive—no other $10k tournament has that many weak players—but the field also includes almost all of the thousand best tournament players in the world.1
But in another sense, the WSOP is brutally difficult compared to a neighborhood tournament. Even if the players had the exact same skill level as your home game tournament, the WSOP would be a much tougher spot to make money. And that’s because of the rake.
Is that even +EV, bro?
At the heart of good decision-making under uncertain conditions is the concept of expected value, or EV for short, which is just the weighted average of all possible outcomes of a choice. Imagine I offered you a choice: you can have $50, or you can roll a die. If you roll the die and it comes up anything but 6, you get $0. If it comes up 6, however, you get $10,000. Some people might take the $50, but most people would choose the die roll. Even though 83% of the time they will get nothing, the expected value of the die roll is $1,366.67; you lose $50 5/6 of the time, but 1/6 of the time you net $1616.67 ($10k/6 - $50). It’s a highly +EV decision to roll the bones in this spot.
Whether you are gambling or investing in the stock market or just trying to wisely choose what route to take to your destination, you often are trying to maximize your expected value, be it in units of money, time, happiness, or just generic utility. This is especially true in situations that repeat, because over the long-run your actual results will eventually converge toward your EV. If you are only given one chance at the $50 die choice from above, I think it would be exceedingly dumb to take the $50, but I get it if you really just want to go out to dinner tonight and your budget doesn’t otherwise allow it.
But if you could play this game repeatedly—i.e. pay $50 each time you wan to roll the die, as many times as you want—it would be batshit insane not to start rolling, and not stop until the moron offering you the choice takes what’s left of his money and goes home.2 Despite this, you’d be amazed at how many people just don’t seem to want to make +EV plays in card games, even when they know it’s the right move.3
Closely related to expected value is the concept of variance. Sometimes you are willing to forego the highest expected value, in order to avoid extreme outcomes. Imagine if you have two vacation choices, same price. Choice A is a week at a nice but not great beach in Florida, and the weather is guaranteed to be perfect. Choice B is a week at the most beautiful beach in the Mediterranean, but there’s a 25% chance it will rain and you will be stuck indoors all week. If you think the Mediterranean vacation is a lot better than the Florida vacation—like two or three times better—assuming the weather holds, then it’s a better EV play. (Imagine Florida is worth 15 to you, sunny Greece is 30, and rainy Greece is 4. That makes the EV of Greece 23.5 (75% * 30 + 25% *4). But maybe you just want to guarantee a decent vacation, without rain. That might lead you to choose Florida. Lowers your EV, but reduces your variance.
This is exactly how all insurance works. You pay a modest amount of money in order to avoid the worst possible outcomes. It’s a negative EV proposition and you are happily taking it to reduce your variance. The only way for the insurance company to make money is to charge more than, on average, than they will pay out in claims. Your expected value is highest to just roll the dice and hope you don’t get cancer in your 20s. But by taking a mildly -EV option—buying a cheap health insurance plan that in all-likelihood you will never use for a big hospital visit—you can avoid the nasty downside of the unlikely $150,000 bill if you need cancer treatment when you are 23.
When people play casino games, they are doing something like the opposite of the insurance play. They are taking a -EV option with the hopes of hitting the unlikely outcome. This is part of the reason why casinos are both popular among people and profitable for the casino. They offer a -EV wager with a very wide variance. A pull on a slot machine has an expected value of something like -8%, meaning you get back 92 cents for every dollar you put in.
It would be supremely stupid for casinos to just payout the exact EV of the slot machines. Imagine putting a dollar in, pulling the lever, and having 92 cents splash out the bottom every time? Nobody would play. Instead, the games are structured so that most of the time, you get nothing when you spin the lever, but once in a while, a whole bunch of money falls out. Same EV, different variance. The precise schedule upon which slot machines pay out, I promise you, has been studied extensively by casinos and set at the point that maximizes the most revenue.4
This is literally how every casino game works. Offer people a -EV bet, but make the variance high enough that in any one play, someone could win a sizable amount of money. Roulette, craps, slot machines, the state lottery. It’s all the same thing, disguised in different ways. And it’s more or less a fool’s errand to hope to profit by playing it. In the long run, you are guaranteed to lose at all of them.
Except for poker.5
In poker, your opponent isn’t the house
If you play poker in your basement with your friends, on any given night you might win or lose. There’s a lot of luck to poker, and good players will have losing night and bad players will have winning nights. That’s sort of what keeps the game popular, the skill/luck balance is almost perfect for a gambling game.
But in the long run, the good players in your basement are going to get the money, because their skill gives them a positive expectation. Unlike the casino games played against the house, poker pits players against other players. Which means it is possible to win.
It’s not easy to quantify poker skill, but the general concept is pretty simple. If we took 10 equally skilled players and had a $20 poker tournament in my basement, where first place got all the money, the results would look like this:
Who actually won this week would essentially be random. All the players are equally skilled, so whoever got the best cards or most luck probably won. Note that everyone has the same expected value here—zero. 90% of the time you will lose $20, and 10% of the time you will win $180. In the long run, this is zero-sum game, and even though you might win the first two times we play, everyone’s long-term expectation is exactly zero. Not positive like our original dice game example, and not negative like the casino games. Just zero.
Now imagine you are skilled at poker compared to your neighbors. Say you have a 20% chance of winning any given tournament. Now the table looks like this:
Four out five times you play, you are still going to lose your $20. But with your skill edge making you a winner a lot more often than average, you now have a positive expected value—$20—although notice that you will never actually win $20, because the only possible outcomes are +$180 and -$20. You just win a lot more than your fair share. And that money comes from the other players. who now have a negative expected value. But note that they too will never lose their EV, they can only win $180 or lose $20. And notice that the total EV of the group is zero: the sum of your winnings and their loses is $0. And this makes intuitive sense: all the money that goes into the game comes back out of the game to the players.
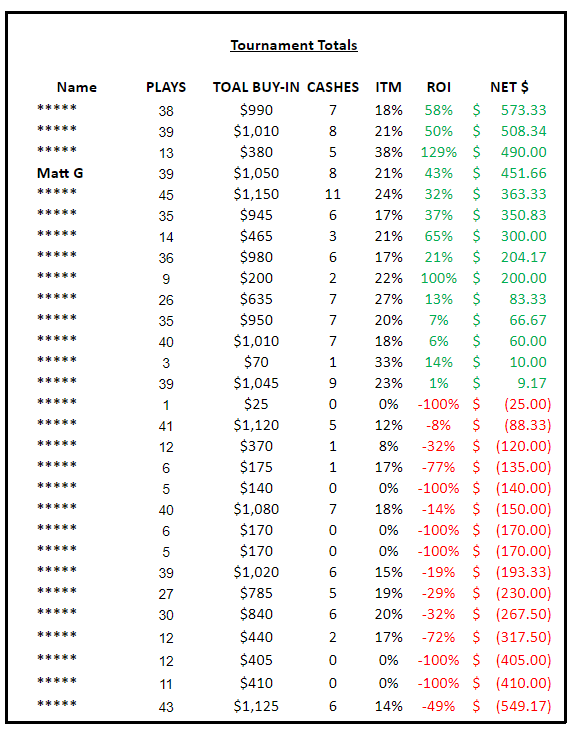
And this is how home poker games work! Here are the (anonymous except for me) results this year from the home poker tournament series I play with my friends:
Looking at the chart, you can see that I’ve played 39 tournaments this year, and it has cost me a total of $1050 to enter them (most of them are $20 or $25 entry fees). In 8 of those 39 tournaments, I’ve won a cash prize, which means I was In The Money (ITM) 21% of the time, as noted on the chart.
Sick brag bro, this means I’ve had a pretty good season! I’ve won $1501.66 in prizes, for a net profit of $451.66, which is a 43% return on my $1050 investment.6 This is decent—but not great—evidence that my EV in this series is positive. It’s a very small sample size. On the other hand, notice that if I am a winning player, I’m still getting no prize in 79% of the tournaments I enter!7
But more importantly, look at the overall picture of this tournament series. Of the 29 players, 14 of them are currently having winning seasons, and 15 are currently having losing seasons. That’s not an uncommon distribution for a home game series. A combination of difference in skill and difference in luck over the course of a year will naturally sort people out. Different players have different EVs in this series, but the overall EV of all the players is zero: every dollar that goes in for the entry fees comes out as a dollar in the prize pool. Collectively, it’s a zero-sum game.
Casino poker is not a zero sum game. Not even close.
Sometimes you’ll hear the stat that 90% of poker players are losing players. Which doesn’t really jive with the home game statistics I’ve just shown above. It’s simply not the case that 10% of the players in my home game series are taking all the money from the other 90%.
Nevertheless, it is true that the vast majority of players—perhaps even 90%—in the public poker rooms across the country are losing players. And this is because public poker is not zero-sum. It’s negative sum.
Unlike my home game series, all the money that goes into the tournament in a casino does not come out. Since you are not playing against the house in a poker tournament at a casino, the casino needs some way to cover the cost of running the tournament and make some profit.8 So the casinos charge a fee—usually called the rake—for playing in the tournament. This money does not go into the prize pool to pay the winners. Instead, it goes directly to the casino. In most poker tournaments, the rake is somewhere between 10% and 20% of the entry fee.
That’s a lot of money. And it dramatically changes the outcomes for the players.
For example, imagine if my home game tournament series was charging a typical rake for a small-stakes live poker tournament, say 20%. In order to maintain the same prize pool, we’d have to increase the entry fee by 25% (so the $20 tournament now cost $25, with the $5 being the 20% that went to the house as a fee). And that fee isn’t just charged to winning players; everyone has to pay it. In effect, we can simulate this buy simply increasing the total buy-in in our home game results chart by 25%. Here’s what happens:

You can see that almost half of the winning players have becoming losing players. The rake turns marginally +EV poker players into marginal losing players. It also greatly reduces the profits for the winning players that remain. Look at my ROI—it drops to a measly 14% as my winnings plummet by almost 60%. Remember, this has nothing to do with the skill of the competition—we’re looking at the exact same home game data. All of the money is just rake going to the casino.
We’ve gone from a zero-sum poker tournament series to a negative-sum series. And it’s a big negative sum; in this hypothetical the players in my club pay $4,861 in rake to the casino. The casino is, by far, the biggest winner in the tournament series.
None of this means casino poker is unbeatable. But it does mean it is much tougher to beat than home game poker, even if you are playing against players of identical skill level. The skill edge required to beat the players alone doesn’t cut it, you need to be able to beat them by enough to also cover the rake.
What are the lessons of this? First, if you are playing poker tournaments with an eye toward winning money, consider the rake. It varies considerably from casino to casino and from tournament to tournament. Tournaments with a rake over 35% are probably straight-up impossible to beat. Tournaments with a rake in the single-digits are much more player friendly.
Second, negative sum games are brutal, and very few people are going to be long-term winners.
Finally, if you are a recreational player, consider starting a home poker game or tournament series. The lack of rake means a lot more players can be winners in the game, and you don’t have to stomach the idea of giving a casino thousands of dollars just to have an expectation of winning hundreds.
(I’ll be sure to update this post after I bink a WSOP event for six figures).
This makes the Main Event pretty bizarre. On Day 1, it’s inarguably the softest 5-figure buy-in tournament in the world. But by the latter stages, when the field is decidedly tilted toward professional players, it becomes a very, very tough field.
Honestly, if you ever actually came across this hypothetical situation in real-life, you might use some Bayesian reasoning to figure the die is rigged and can never roll a six. Always be wary of people offering you bets that seem utterly too good to be true.
A classic one afflicts several of my family members in casual games of Bridge. They refuse to bid for the huge game bonus, because they’d rather make their hand. But making the game bonus 50% of the time has a much higher EV than making a part-score 100% of the time.
Sadly, the revenue-maximizing point for slot machines is almost certainly the one that targets gambling addicts.
And a few other things, like sports betting.
And an hourly rate of like $5. Like I said, sick brag.
If you can’t stomach losing 4 out of 5 times you play, tournament poker is not for you.
It’s not clear all poker rooms at casinos make money. It’s entirely possible that some are setup as loss leaders for the games that make the casinos a lot more money. In any case, even when poker rooms are profitable, they aren’t nearly as profitable as other parts of the casino.







I used to play poker with friends, but I've never been to a casino, so one thing I've always been curious about is the issue of tipping the dealer. What I've read online seems to suggest that tipping the dealer is as customary as tipping a waiter, and not tipping would be as sociopathic as not tipping a water. And also that you need tip in tournaments (if you win money) as well as cash games. So it's really the case if you are not a sociopath, then the situation is even worse than it looks?